分布

偏った分布(Skewed) ＝非正規分布ではMedianを用いて表す。

偏っていない分布＝正規分布ではMeanを用いて表す。

 

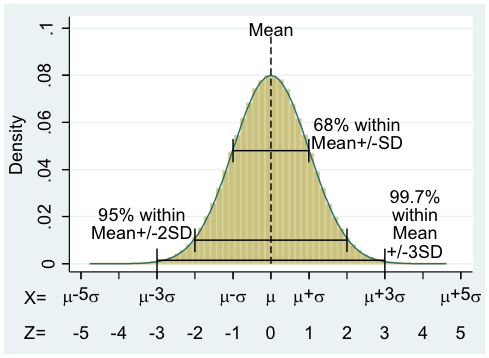
正規分布である、ある集団において、Meanと標準偏差(Standard Debiation、SD)が求めらた場合、その集団に属する人達は

Mean+/- SD以内に68%

Mean+/- 2SD以内に95%の確率で存在(正確には1.96SD)(95%信頼区間 95%Confidence Intervals)。

Mean+/- 3SD以内に99.7%の確率で存在するという事になる。

例えば、値が＋３SD以上である確率は、片側のみの計算となるため0.15％というなる。

Z Distribution

ちなみに上記で±1-3の値が代入された箇所はz valueと呼ばれ、SDと掛け合わす事により平均からの距離を表す。zの値が任意のZより小さい確率は下記のZ distributionとなる。

z value	0.5	0.68	1	1.5	1.96	2
P(Z>z)	0.309	0.248	0.159	0.067	0.025	0.023

 

Uncertainty intervals：

標準誤差（Standard Error、SE）は集団を超えた全体の平均値（population mean, µ）を集団の平均値から推測する際の正確性Precisionの指標である。

Population mean、µは± 2SEの範囲の中に95%の確率で存在する（Uncertainty intervals）。これはどういうことかと言うと、全体の中から、繰り返し無作為に集団を取り出して± 2SEを計算することを100回繰り返すと、作り出した信頼区間のうち、95個に全体の平均値が含まれるという意味である。

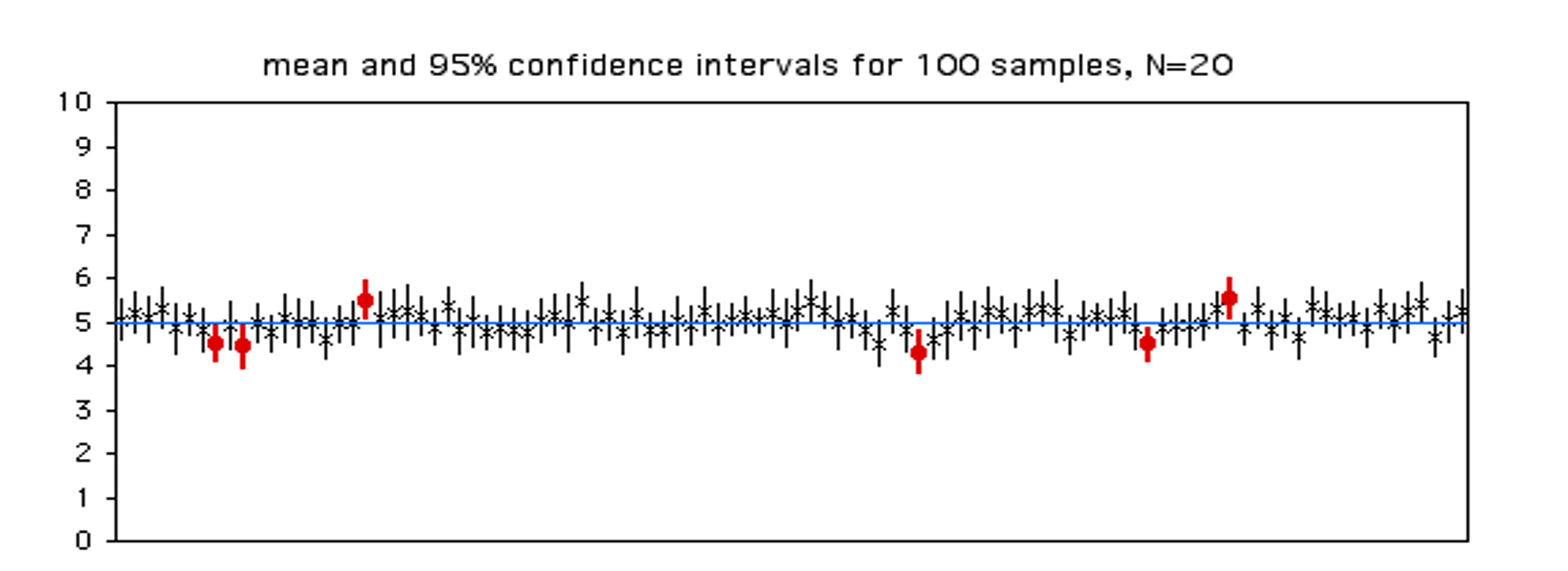
青線がpopulation mean、100個ある縦棒はそれぞれ取り出した際の95％信頼区間。赤の縦棒にはpopulation meanが含まれていない。この赤棒の数は5個である。

Mean+/- 2SDはサンプル内の個人、Mean+/- 2SEではサンプルを超えた全体を指している大きな違いがあることに注意である。

論文中では、テーブル・本文には散らばりを表すため変数毎のMean, SDを表記し、グラフで推移を表す際はサンプルを超えたより一般的な全体の推移を表すため2SEのひげ（95%信頼区間）を表記することが一般的である。

指標

Crude mortality rate：全死亡数／全人口数

Cause-specific mortality rate：その原因による死亡数／全人口数

Attack rate：イベントの発生する率

Case fatality rate：イベントの発生した群の中で致死となった割合。

Standardized mortality ratio：観察された死亡数／予想された死亡数

Standardized incident ratio：observed case number / expected case number

Maternal mortality rate：母体死亡数／出産数

Crude birth rate：出生数／全人口数

多重性(Multiplicity)

RCTなどで、副次評価項目等で、仮説検定を繰り返すことによってType 1 (アルファ) エラーを引き起こすこと。5%を有意水準とする場合、検定を5回行えば、23 %（=1-0.95⁵）でどれかが有意な結果をもたらす。

 

絶対リスク減少率 abuslute Risk Reduction (ARR)

ARR=非介入群の発生率ー介入群の発生率

 

相対リスク減少率 Relative Risk Reduction (RRR)

RRR=ARR/ 非介入群の発生率

 

相対危険 Relative Risk (RR)

RR=介入群の発生率 / 非介入群の発生率

 

Number Needed to Treat (NNT)

NNT= 1 / ARR

例：

治療群でアウトカム発生率５%

プラセボ群でアウトカム発生率２０％　の場合

ARR=20-5=15%

RRR=15/20=0.75

RR=5/20=0.25

NNT=1/0.15=6.67人

Clinical Significance

有意な結果であったとしても、臨床的に意義の無い差であること。この基準は疾患やコンテクストによる。

例：新規の降圧薬の降圧効果は0.5mmHgで有意差を認めた。しかし、この血圧の差は臨床的に意義はないと考えられる。

妥当性 Validity

体型的な systematic（研究のシステムに内在された）エラー（真の相関関係から離れてしまう事）が無いこと。サンプルサイズ(random error)とは関係はない。

内的Internal: バイアス bias(selection, Information), 交絡因子Confounding

外的External: 一般化できるかどうか generalizability

正確性 Precision

＝信頼性Reliability=再現性Reproducibility

ランダムエラーが無いこと。繰り返し行って、同じ結果が得られること。

帰無仮説 null hypothesis

	Reject H0	Don’t reject H0
H0 is true	Type I error、 α False positive	True negative 1-α
H1 is true	True positive 1-β	Type II error、 β False negative

H0帰無仮説、H1 Alternative hypothesis

	H1 is true	H0 is true
Reject H0	True positive Power=1-β	Type I error、 α False positive
Don’t reject H0	Type II error、 β False negative	True negative 1-α

H0帰無仮説、H1 Alternative hypothesis

Power= 1-β：パワーはサンプルサイズの増加、αの増加（有意水準を下げる）、標本の差の増大によってPowerは増える。

Type 1 エラー：α＝統計的有意水準

Type 2 エラー：帰無仮説が真でない時に、帰無仮説が棄却できない事。研究のパワー＝サンプルサイズに依存し、増えれば、タイプ２エラーは減る。

p value

帰無仮説が起こりうる確率＝違いが無いという確率。値により以下のように解釈される。

0.1>P>0.05 weak evidence,

0.05>P>0.01 evidence,

0.01>P>0.001 strong,

0.001>P very strong

 

バイアス Bias

選択バイアス Selection bias:

研究薬・手技およびその結果に影響を与える不適切な研究対象を選ぶ事、不十分な研究対象の維持により、真の関係性と研究結果が異なること。

No bias to OR if sampling fractions differ only by case-control or exposure status not by both

Sampling (Ascertainment) bias：非ランダム的なエンロールメントのために、適正な研究対象とは異なる事。

Berkson’s bias：病院ベースのケースコントロール研究で適正な研究対象から異なる事 (hospital-based CC study is more likely exposed to exposure)

Healthy worker effect：労働者を対象としたcohort研究にて。働いている労働者は基本的に健康であるため、疾患、死亡が少ない。

Allocation Bias：治療群、コントール群に割り当てる際に生じるバイアス。例えば、非ランダム的に、より重症患者を治療群に割り当てること

Prevalence (Nyeman) bias：Exposureが非常に前になるために、疾患発症確認をする前に死亡するなどで、疾患発症が見逃されること。

Attrition Bias：著しく参加者がフォローアップの期間中に減る事によって生じるバイアス

観察バイアス Misclassification bias / Observational Bias

Information bias： 収集データの定義の曖昧性やデータ収集方法の不備によるバイアス。

Interviewer bias：ケースコントロール試験で、アウトカムを知っているinterviewerによって生じるバイアス。画一的な質問表を用いることで減らす事ができる。

思い出しバイアス Recall bias： レトロスペクティブ研究で多い。否定的なアウトカムはExposure群で報告されやすい。

Observer Bias：治療割当を知っていることによる結果覚知への影響、もしくは観察者が分類エラーすることによる発生。

Reporting bias：社会的なスティグマからexposureが過大、過小報告されること。

Verification bias=workup bias　検査陽性の患者のみに侵襲的検査を行うことによって感度が過大・過小評価される事。

オッズ比への影響

観察バイアスの性質によってRelative riskへの影響の方向が変わる。

non-differential (errors in determining exposure status or results, but occur equally among cases and controls or exposed and unexposed)=オッズ比は１に向かって近づく

differential (occur unevenly)=オッズ比は１から離れる方向に動く

混合バイアス Mixed bias

selection biasと Observational biasの混合したもの

Surveillance (detection) Bias：有リスク群、Exposure群でモニタリングが増え、結果、アウトカムの発生が増えること。cohort研究で起こりうる。

他

Hawthrone Effect：被験者が観察されている事を自覚することにより、行動の変化が出てしまうこと。内部妥当性に影響を与える。

プラセボ効果 Placebo Effect：患者の期待感より結果に影響が認められること。

 

スクリーニングに関連するバイアス

Lead-time bias: 従来よりも早期発見されることにより、実際の治療経過は変わらないも関わらず、生存期間が伸びたと誤認すること

Length-time bias: 広がりの少ない、もしくは進行の遅いタイプをより発見することにより、生存期間の伸びたと誤認すること。進行の早いタイプはスクリーニングの前に死亡して発見されない。

Compliance bias(selection bias): screened patients are better educated and more health conscious

 

交絡因子Confounderと多変量解析 Multivariate analysis

交絡因子Confoundersとは、Exposureとアウトカムに影響を与え、真のAssociationに影響を与えうる他の独立変数のこと。バイアスの一種(Confounding Bias)。Confounderのコントロールの方法は２つ。Multivariate analysisでadjustを行うか、

Multivariate analysisでは、univariate analysisで考慮されない交絡因子をAdjustできる。交絡因子の場合、Stratificationを行った場合に効果量に差は認めない。（これがEffect Modifierとの大きな違い）

例：子供の身長とIQの関係において、年齢は身長とIQともに影響を与える交絡因子である。この場合、年齢でStrafticationすると身長がIQに与える効果量は有意ではなくなる。

 

Effect Modification (Interaction)

Stratificationを行ってそれぞれのリスク比を表す。多変量解析でのAdjustmentでは調整できない。例えば糖尿病の有無によって糖尿病とは関係の無い疾患の薬の効きに差がある場合は、Stratificationを行う必要がある。糖尿病の有無自体が薬の投与する・しないことに差を生じないため、交絡因子とは言えない。

因果関係 Causality

因果関係を示唆する要素

類似性 Analogy：似たようなAssociationが知られている事

生物学的勾配 Biological Gradient：原因と結果に用量依存性Dose response relationshipがある事

生物学的妥当性 Biological Plausibility：既知の知識から説明がつくこと。

一致性 Coherence：Associationが既知の事に矛盾しない事

一貫性 Consistency：原因は広い範囲で結果に関係している事

実験的証拠 Experimental evidence：実験的なデザインで証明されている

特異性 Specificity：原因は特異的に結果に関連している

関連の強さ Strength of association：関連が強い事

時間 Temporality：原因が結果に先行すること

エコロジカルスタディ Ecological Study

Ecological fallacy：エコロジカルスタディの結果はポピュレーションレベルの情報であるため、それを個人レベルに適応する事はバイアス （Ecological fallacy）を生む。

クロスセクショナルスタディ Cross-Sectional Study

ExposureとOutcomeの関係を同一の時間のタイミングで調査する事。そのため、Prevalence Studyとも言われる。

ケースコントロールスタディ Case Control

稀な疾患によい適応となる。研究対象となるOutcomeがすでに決まっている場合に、Exposureの探求のために行う。例えば食中毒の原因調査等。

思い出しバイアス(recall bias)によるExposureのMisclassificationのリスクあり。 

 

	Cases	Controls
Exposed	A	B	Nexp=A+B
Not exposed	C	D	Nnoexp=C+D
	Ncase=A+C	Ncont=B+D

オッズ比 Odds ratio

OR=Odds of disease among exposed / Odds of disease among not-exposed

=( A/A+B / B/A+B ) / ( C/C+D / D/C+D )

=(A/B) / (C/D) =AD/CB

コホート研究

研究対象のExposureがすでに決まっている場合に行う。

 

	Cases	Non-Cases	Incidence of Dx
Exposed	A	B	Iexp=A/A+B
Not exposed	C	D	Ine=C/C+D

リスク比 Relative risks /or risk ratio (RR)

RR=incidence in the exposed/ incidence in the unexposed=  Iexp / Ine

Attributable Risk (AR)

=Iexp – Ine

Attributable Risk Percent

＝暴露された群の疾患発生のうち、暴露が寄与する割合

=AR/Iexp

Population Attributable Risk Percent (PARP)

=全体での疾患発生のうち、暴露が寄与する割合

＝(全体での疾患リスク-Ine) / 全体での疾患リスク

*全体での疾患リスク＝Iexp x 暴露群の全体に占める割合 + Ine x 非暴露群の全体に占める割合

 

RCT

Net Clinical Benefit

介入によるメリットから介入によるデメリットを差し引きしたもの

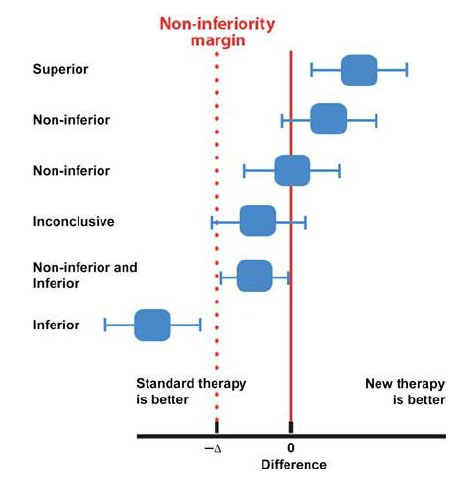
非劣性試験

non-inferior marginを用いて判定を行い、95%信頼区間がこのMarginを超えていなければ、非劣性と判定される。

 

感度・特異度

	疾患あり	疾患なし
テスト陽性	TP	FP
テスト陰性	FN	TN

感度(Sensitivity)：疾患がある人の中でテスト陽性の割合　＝TP/(TP+FN)

特異度（Specificity）: 疾患がない人の中でテスト陰性の割合　＝TN/(TN+FP)

偽陽性（False positive）: FP/(TN+FP) = 1- Specificity

偽陰性（False negative）: FN/(TP+FN) = 1- Sensitivity

* 分母は疾患のありなしの数

* 疾患の頻度によってこれらは影響を受けない

的中率

陽性的中率（Positive Predictive Value）: テスト陽性の中で真に疾患がある人の割合　＝ TP/(TP+FP)

陰性的中率（Negative Predictive Value）: テスト陰性の中で真に疾患がない人の割合　＝TN/(TN+FN)

*これらは疾患の頻度に強く影響される

*陽性適中率（Positive Predictive Value）と感度（Sensitivity）がもっとも重要なパラメーターである。

陽性尤度比（Positive likelihood ratio, LR+）

= 感度／（１−特異度）= TP/(TP+FN) ÷ FP / (FP+TN) = TP/FP ÷ (TP+FN)/(FP+TN) = 検査後オッズ／検査前オッズ  

＝”検査陽性の判定があれば、検査後にどれだけ疾患陽性の患者が変化したか”という指標。

＝”疾患の無い被検者が陽性となる確率と比べ、疾患のある被検者が検査陽性となる確率”

陰性尤度比（Negative likelihood ratio, LR-）：

= （１−感度）／特異度

 

LR+は１０以上で強い有用性、5-10で中等度、2-5で弱い有用性と判断される。

LR+、LR-ともに0.5-2はエビデンスなし

LR-は0.1以下で強い有用性、0.1-0.2で中等度、0.2-0.5で弱い有用性と判断される。

＊ 疾患の頻度によってこれらは影響を受けない

 

 

 

検定

検定の選び方

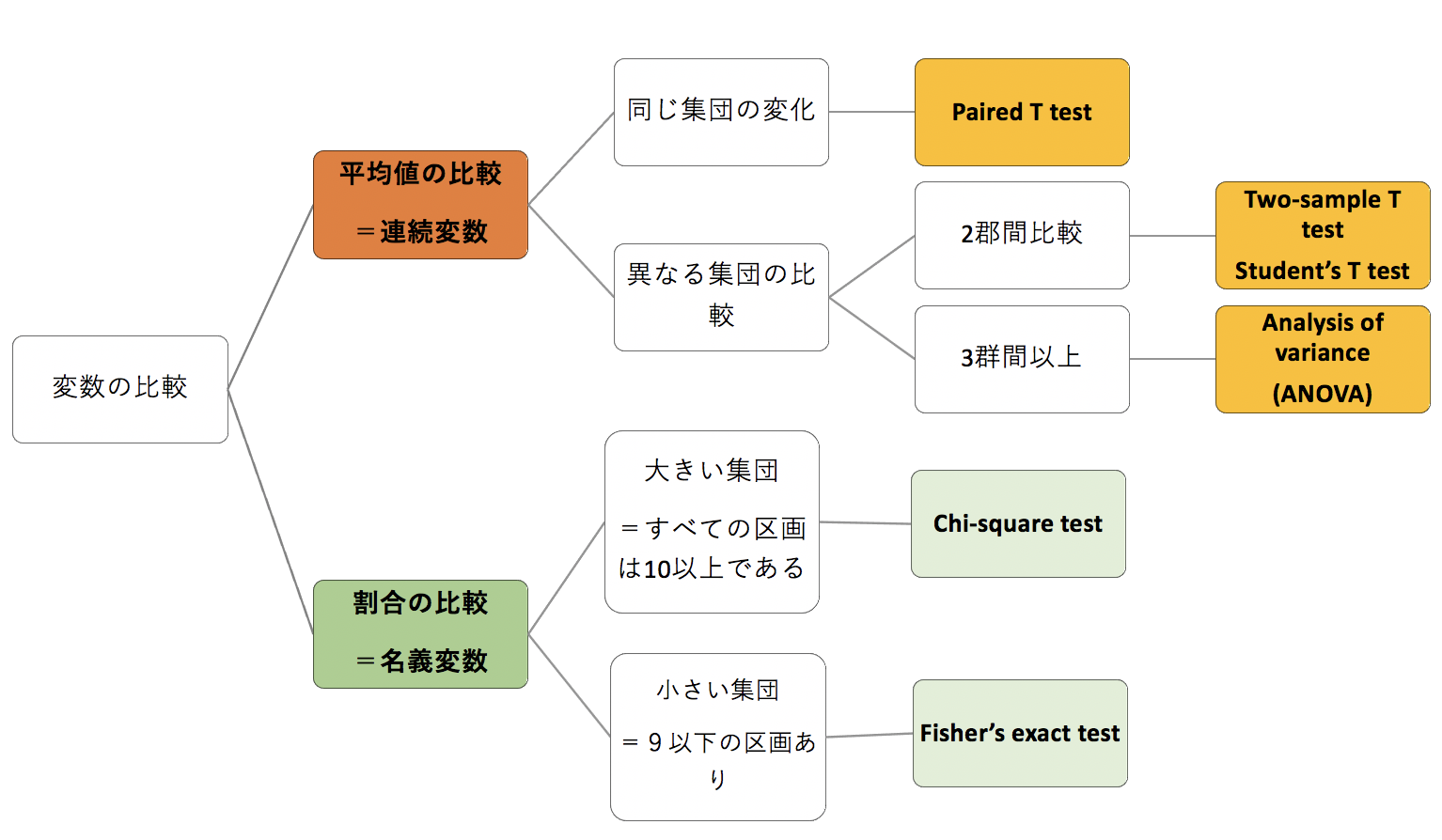
２群間での平均値の比較＝連続変数の比較

	Paired	Unpaired
正規分布	Paired t-test	Unpaired t-test
非正規分布	Wilcoxon t-test	Mann-Whitney U-test

多群間での平均値の比較＝連続変数の比較

	Repeated measures	Non-repeated measures
正規分布	Repeated measures ANOVA	Non-repeated measures ANOVA
非正規分布	Friedman’s X2r-test	Kruskal Wallis H-test

割合の比較＝名義変数の比較

すべてデータ数は10以上	9以下のデータ数あり
2×2 Chi square test	Fisher exact probability
mxn Chi square test

２つの連続変数間の回帰分析

正規分布	Correlation
非正規分布	Spearman’s correlation

 

 

カイ二乗検定 Chi-Squared test：

２つ以上のカテゴリカル変数の比較。

帰無仮説＝分布はすべてにおいて等しい

トレンド分析

２x mの場合で、mとなるのが順序変数（それぞれに順序関係のある名義変数、例えば年齢で３群以上にグループ分けした場合のある疾患の頻度を比較する場合等）の場合に、カイ二乗トレンド分析を用いて検定を行う事ができます。

フィッシャー正確性検定 Fisher’s exact test：

２つのカテゴリカル変数の比較で、一つのグループ（例えば、Aあり、Bなしのグループで）のn数が１０以下の場合に用いる。

McNemar検定：

ペアでの割合の比較　（同じ群での治療前後でのあり・なしの比較）

Paired t-test：

ペアでの平均値の比較（同じ群での治療前後での血圧の比較）

ANOVA (ANalysis Of VAriance)：

等分散、等分布、正規分布を前提とした多群比較。F statistic

 

Kappa Statistic：

検査者間の信頼性の定量的評価。Kappa値が>80でExcellent、0.61-0.8でgood、0.41-0.60でfair、0.21-0.40でminimal、0.20以下で偶然の一致と同等と評価される。

 

Sensitivity analysis

解析対象をある基準で選別して、主分析を繰り返し、それにより結果の堅固性 Robustnessを評価すること。

 

線形回帰分析 Linear Regression

y=α+βx,

α=intercept (average y when x=0),  β=slope, regression coefficient

Null hypothesis H0: β=0、T statistics, T distribution

Correlation (Correlation Coefficient)

r=0 no linear association,

r=1 perfect positive assoc. 陽性的中率が高いと言える

r=-1 perfect negative assoc.

決定係数 Coefficient of determination = r²

アウトカムの変動がどれだけの％で説明変数によって説明できるかという指標。

ｒ^２＝１−　残差の二乗和 / 偏差の二乗和

r=0.5であれば、25%のアウトカムの変動 Variabilityは説明変数によって説明される。

残差　Residual

実測値 ー regressionによる計算値

多変量解析